Hexadecimal Numbers
So far we have looked at two number systems – base 2 (binary) and base 10 (decimal). Another common number system used in Computer Science is base 16, otherwise known as hexadecimal, or hex for short.
Why do we use hex? Well, it’s a multiple of 2, so it is relatively easy to convert between binary and hex, and hex values are more human readable and understandable than the longer binary values.
Because hex is good at representing very large binary values it is used in many areas of computing, like character encoding, memory addressing, RGB colour values and IPv6 addresses.
In this lesson, we’ll learn about:
- What hexadecimal notation is.
- How to convert numbers from decimal to hexadecimal.
- How to convert numbers from hexadecimal to decimal.
- How to convert numbers from binary to hexadecimal.
- How to convert numbers from hexadecimal to binary.
1. What is Hexadecimal Notation?

Hexadecimal notation is a numbering system like binary and decimal, but everything goes up in multiples of 16.
However, because our decimal numbering system only goes from 0-9, we use the letters A-F to represent the remaining numbers, as shown in the table below.
Just like you did with binary, the best way to get this right is to write down your Hex table before you start.
| Decimal | Hex Value |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| Decimal | Hex Value |
|---|---|
| 8 | 8 |
| 9 | 9 |
| 10 | A |
| 11 | B |
| 12 | C |
| 13 | D |
| 14 | E |
| 15 | F |
So in hexadecimal, the number 6 is 6 just like decimal, but the number 14 is E.
Further Thought
In the lesson introduction we saw some of the ways hex is used in computing. Research more about these and why hex is so important.
2. How to Convert Decimal to Hex
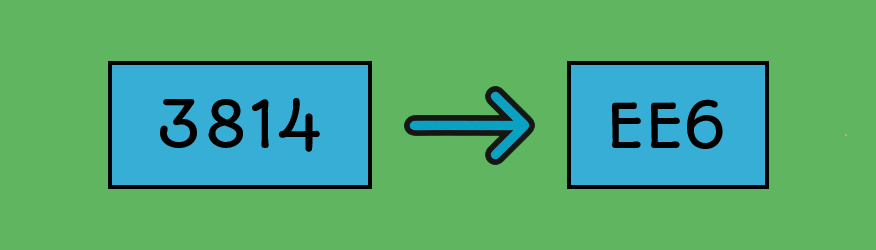
To find out the hex value of a decimal number we follow a similar process to working out the binary.
The difference between binary and hex conversions is that now we have to work out how many TIMES the column number will fit into our desired number.
Remember, with binary each number to the left increases in multiples of 2. But with hexadecimal it increases by multiples of 16. So our columns are as follows:
| 4096 | 256 | 16 | 1 |
|---|---|---|---|
Worked Example 1
Let’s work out the hex value for the decimal number 20.
Just like converting to binary, we ask similar questions and follow a similar process:
Will 4096 fit into 20? No, so we don’t have any of these, so we put a 0 in the 4096 column.
| 4096 | 256 | 16 | 1 |
|---|---|---|---|
| 0 |
Will 256 fit into 20? No, so we don’t have any of these, so we put a 0 in the 256 column.
| 4096 | 256 | 16 | 1 |
|---|---|---|---|
| 0 | 0 |
Will 16 fit into 20? Yes. How many times? 1 – so we put 1 in the 16 column.
| 4096 | 256 | 16 | 1 |
|---|---|---|---|
| 0 | 0 | 1 |
Now we have to take 16 away from 20. 20 – 16 = 4.
Will 1 fit into 4? Yes. How many times? 4 – so we put 4 in the 1 column.
| 4096 | 256 | 16 | 1 |
|---|---|---|---|
| 0 | 0 | 1 | 4 |
So, the hex value for 20 is 14 (and you say it as ONE – FOUR). Don’t worry if that’s a bit confusing – let’s try another example with a larger number.
Worked Example 2
Let’s work out the hex value for the decimal number 109.
Will 4096 fit into 109? No, so we don’t have any of these, so we put a 0 in the 4096 column.
| 4096 | 256 | 16 | 1 |
|---|---|---|---|
| 0 |
Will 256 fit into 109? No, so we don’t have any of these, so we put a 0 in the 256 column.
| 4096 | 256 | 16 | 1 |
|---|---|---|---|
| 0 | 0 |
Will 16 fit into 109? Yes. How many times? 6 – so we put 6 in the 16 column.
| 4096 | 256 | 16 | 1 |
|---|---|---|---|
| 0 | 0 | 6 |
6 x 16 is 96, so we have to take 96 away from 109. 109 – 96 = 13.
Will 1 fit into 13? Yes. How many times? 13 of course, but what is the hex code for 13? Using the table near the start of this lesson we can see that it is D.
So we put D into the 1 column.
| 4096 | 256 | 16 | 1 |
|---|---|---|---|
| 0 | 0 | 6 | D |
So, the hex value for 109 is 6D.
Worked Example 3
Let’s try one last number. A really big one this time. Let’s try 5078.
Will 4096 fit into 5078? Yes. How many times? 1 – so we put 1 in the 4096 column.
| 4096 | 256 | 16 | 1 |
|---|---|---|---|
| 1 |
Now we have to take 4096 away from 5078. 4096 – 5078 = 982.
Will 256 fit into 982? Yes. How many times? 3 – so we put 3 in the 256 column.
| 4096 | 256 | 16 | 1 |
|---|---|---|---|
| 1 | 3 |
3 x 256 is 768, so we have to take 768 away from 982. 982 – 768 = 214.
Will 16 fit into 214? Yes. How many times? 13 – but what is the hex code for 13? Using the table near the start of this lesson we can see that it is D.
So we put D in the 16 column.
| 4096 | 256 | 16 | 1 |
|---|---|---|---|
| 1 | 3 | D |
13 x 16 is 208, so we have to take 208 away from 214. 214 – 208 = 6.
Will 1 fit into 6? Yes. How many times? 6 – so we put 6 in the 1 column.
| 4096 | 256 | 16 | 1 |
|---|---|---|---|
| 1 | 3 | D | 6 |
So, the hex value for 5078 is 13D6.
Further Thought
What do you think would come after the 4096 column? See if you can work it out and check your answer online.
3. How to Convert Hex to Decimal

Converting from hexadecimal to decimal is straightforward. All we need is our hex table from the beginning of this lesson.
Let’s look at the example below:
| 4096 | 256 | 16 | 1 |
|---|---|---|---|
| 0 | 0 | D | 9 |
We have nothing in the 4096 and the 256 columns, so we can leave those alone.
We have D in the 16 column. We can see from our hex table that D is the hex value for 13. So we need to multiple 13 x 16, which gives us 208.
In the 1’s column we have 9, which we don’t need to do anything to.
Now we just need to add these numbers together. 208 + 9 = 217.
So, the decimal value for D9 is 217.
Further Thought
Mastering hex to decimal conversion is simple, but does take some practice. It helps if you learn the 0-F numbers by heart. Practice this with a friend.
4. How to Convert Binary to Hex
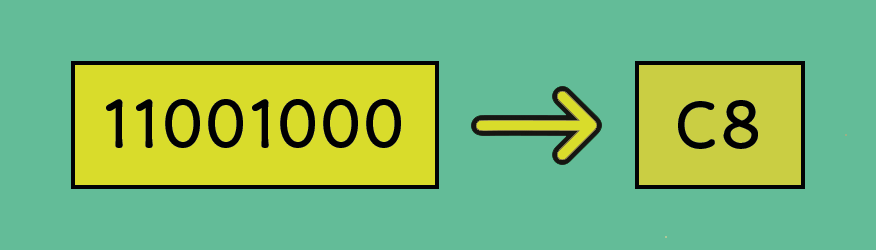
In a previous lesson we learned that a nibble was 4 bits. The smallest number we can store in 4 bits is 0.
| 8 | 4 | 2 | 1 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
The largest number we can store in 4 bits is 15.
| 8 | 4 | 2 | 1 |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
In hex, each column goes from 0 – 15, therefore each column can be represented as a nibble.
Here’s how we do this:
Worked Example 1
Let’s take the binary number 100011.
What we need to do is turn these 6 bits into two 4-bit nibbles. This means we’ll need to add two 0’s to the left side of this number to give us 7-bits in total. This gives us:
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
Now, let’s split this into two separate nibbles and treat them as two separate binary numbers.
| 8 | 4 | 2 | 1 |
|---|---|---|---|
| 0 | 0 | 1 | 0 |
| 8 | 4 | 2 | 1 |
|---|---|---|---|
| 0 | 0 | 1 | 1 |
We can then convert these two numbers easily into hexadecimal by adding up the column values that have 1’s in them, just like we do in binary to decimal conversion.
The first number is equal to 2.
The second number is equal to 3.
So, the binary number 100011 in hexadecimal is 23. Note, that’s TWO-THREE, not twenty-three.
Worked Example 2
Consider the number 11101010.
This is already 8 bits, so we can straightaway split it into our two nibbles.
| 8 | 4 | 2 | 1 |
|---|---|---|---|
| 1 | 1 | 1 | 0 |
| 8 | 4 | 2 | 1 |
|---|---|---|---|
| 1 | 0 | 1 | 0 |
We now can convert these two nibbles into their hexadecimal values.
The first number is equal to 14, which in hexadecimal is E.
The second number is equal to 10, which in hexadecimal is A.
So, the binary number 11101010 in hexadecimal is EA.
Further Thought
What would you do if you had a 9-digit binary number? If you aren’t sure, research the answer online.
5. How to Convert Hex to Binary

Yet again we need to understand that each hex column can be split into a binary nibble – a number that goes from 0 – 15.
Let’s say you have a hex number, we’ll use 4D.
What we need to do is recognise that these are two individual nibbles, and so we work out these separately.
First, we convert the number 4 into binary.
| 8 | 4 | 2 | 1 |
|---|---|---|---|
| 0 | 1 | 0 | 0 |
Then we convert D, which is the 13 in decimal, into binary.
| 8 | 4 | 2 | 1 |
|---|---|---|---|
| 1 | 0 | 1 | 1 |
The we simply stick them together.
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
Further Thought
What is the largest binary number you can represent with two hex digits?
Lesson Summary
So to summarise what we’ve learnt in this lesson:
- Hex notation involves columns that are multiples of 16.
- Hex is used to make long binary sequences easier to read.
- Hex is used in IPv6 and in memory addressing.
- The numbers 10 – 15 are represented by the letters A – F in hex.
- To convert from decimal to hex we need to work out how many TIMES the column number will fit into our desired number.
- To convert from hex to decimal, we multiply the number in each column by the column value.
- Converting to and from binary involves treating each column as a nibble.
